7534. Замкнутое сокровище

Группа из n бандитов спрятала украденное сокровище в комнате. Дверь в комнату следует отпереть, только когда понадобится вынести сокровище. Так как бандиты не доверяют друг другу, они хотят иметь возможность открыть комнату и унести украденное только если этого захотят не менее m из них.

Они решили разместить несколько замков на двери таким образом, чтобы она открывалась только когда открыты все замки. Каждый замок может иметь до n ключей, распределенных среди некоторого подмножества бандитов. Группа бандитов может открыть замок, только если кто-то в группе имеет ключ к этому замку.

По имеющимся значениям n и m определить такое наименьшее количество замков, что если ключи от них правильно распределить среди бандитов, то каждая группа состоящая из не менее чем m бандитов сможет открыть все замки, но никакая группа из меньшего числа бандитов открыть все замки не сможет.

Например, если n = 3 и m = 2, то достаточно 3 замков - ключи от замка 1 получают бандиты 1 и 2, ключи от замка 2 получают бандиты 1 и 3, ключи от замка 3 получают бандиты 2 и 3. Ни один из бандитов не может открыть все замки самостоятельно, но любая группа из 2 бандитов может открыть все замки. Можно убедиться, что 2 замков для этого случая не достаточно.

Вход. Первая строка содержит количество тестов. Каждая следующая строка является отдельным тестом и содержит два числа n (1 ≤ n ≤ 30) и m (1 ≤ m ≤ n).

Выход. Для каждого теста вывести в отдельной строке минимальное количество необходимых замков.

Пример входа	Пример выхода
4 3 2 5 1 10 7 5 3	3 1 210 10

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Минимальное количество необходимых замков равно . Тогда любая группа из m бандитов сможет открыть дверь (все замки), но никакая группа из меньшего числа бандитов не сможет проникнуть в комнату с сокровищем.

Пример

Пусть имеется n = 4 бандита.

При m = 1 количество замков равно = 1. Каждому бандиту следует дать ключ от единственного замка:

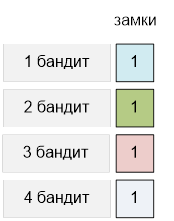
При m = 2 количество замков равно = 4. Ключи от замков 1, 2, 3, 4 среди бандитов следует распределить следующим образом:

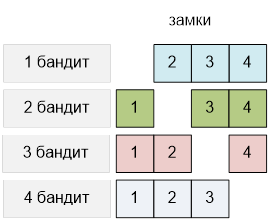
Любые два бандита смогут открыть все четыре замка и забрать сокровище.

При m = 3 количество замков равно = 6. Ключи от замков 1, 2, 3, 4, 5, 6 среди бандитов следует распределить следующим образом:

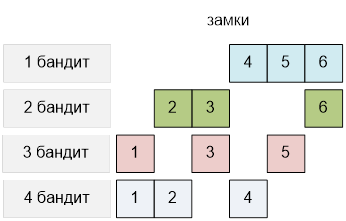
У любых двух бандитов не будет хватать ключа всего лишь от одного замка. Любые три бандита смогут открыть все шесть замков и забрать сокровище.

При m = 4 количество замков равно = 4. Ключи от замков 1, 2, 3, 4 среди бандитов следует распределить следующим образом:

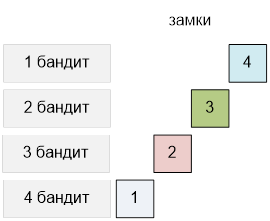
Для того чтобы открыть все 4 замка, каждый бандит должен принести его единственный уникальный ключ.

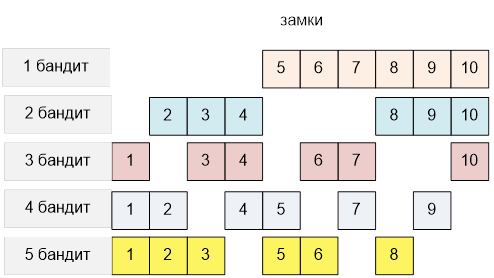
Рассмотрим случай n = 5, m = 3. Количество замков равно = 10. Оптимальное распределение замков среди бандитов следующее:

Реализация алгоритма

В ячейках cnk[n][k] вычислим значения .

#define MAX 31

long long cnk[MAX][MAX];

Заполним массив cnk биномиальных коэффициентов.

void FillCnk(void)

{

int n, k;

memset(cnk,0,sizeof(cnk));

for(n = 0; n < MAX; n++) cnk[n][0] = 1;

for(n = 1; n < MAX; n++)

for(k = 1; k <= MAX; k++)

cnk[n][k] = cnk[n-1][k] + cnk[n-1][k-1];

}

Основная часть программы. Читаем входные данные и выводим ответ.

FillCnk();

scanf("%d",&tests);

while(tests--)

{

scanf("%d %d",&n,&m);

printf("%lld\n",cnk[n][m-1]);

}